Let’s imagine you want to know the price impact of a specific event/DAO decision on the GNO/DAI price.
We will explorer again how conditional tokens can do that.
First again a reminder of the basics:
We can use the conditional token framework to take a DAI and split it into DAI-Yes and DAI-NO. Either of those tokens will pay out a DAI depending on whether or not yes or no happens. Because we can do this split (and also merge = converting DAI-yes and DAI-No back into DAI) at any time at no costs we can establish the price of DAI yes + DAI no == DAI
With those 3 tokens (DAI, DAI yes, DAI no) we can allow trading them against each other. In theory with 3 different tokens, we can establish 3 prices DAI-yes ↔ DAI; DAI-no ↔ DAI and Dai-yes ↔ DAI-no - in reality however there should be only 1 price and the other 2 prices can be derived with the mechanic (split/merge) introduced above.
All of this 3 prices should reflect the likelihood of the event/decision happening/ or not.
On Omen markets are established in the form DAIyes ↔ DAINo using the CPMM (from @alanlu/ prominently used by balancer/ Uniswap)
In the next step, we can use GNO in the same way as DAI and introduce thus 3 more tokens (GNO, GNOyes, GNOno)
By introducing 3 more tokens we have a total of 6 tokens and thus up to (6*5)/2 = 15 trading pairs/ prices.
However - in reality, we only have 3 degrees of freedom/ 3 prices that can be set by the market - all others can be derived from 3.
The pair that is easiest to understand is DAIYes / GNOYes. While in previous markets traders would have to make an assumption about the likelihood of yes occurring this likelihood is factored into BOTH DAIYes and GNOYes and thus is irrelevant for the ratio (price) of the 2 tokens.
Speaking form a user perspective:
A user can take $1000 DAI and convert them into 1000$ DAIYes and 1000 $DAINo. Now they take the $1000 DAIYes and buy GNOYes. They will end up with GNOYEs and 1000 $DAINo. The outcome is: if the decision is not made - they will just be able to get 1000$ DAI back (basically nothing has happened) but if the decision is made/ the event happened they have bought GNO at a specific price.
Soon™ Gnosis Protocol V2. will allow to trade all of those 15 pairs and inherently find consistent prices across them. Meanwhile, there are different options to set up those markets:
You could have one CPM AMM with DAIYes, DAINo, GNOYes, GNONo. Alternatively have 3 uniswap markets: DAIYes/GNOYes, DAINo/ GNONo and finally DAI/GNO
Since we are coming from Omen (vanilla prediciton market usecase) for GnosisDAO we will go with the options: DAIYes/DAINO; GNOYes/GNONo and as a third market the generally existing DAI/GNO markets.
Practically this will make it harder for a user to do the conditional investing described above - but it is still possible:
The steps are:
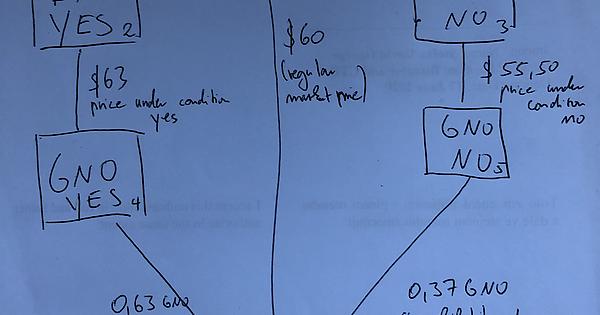
a) buy 1000No DAI (with e.g. 400 DAI)
(Omen allows you to do this - under the hood, you convert DAI to DAIYes and DAINo and then you trade all DAIYes for more DAINO)
Now in case “No” happens you get the full refund
b) with your remaining 600 DAI buy GNO on a regular market
c) Use all the GNO to buy GNOYes
In the end, you will hold 1000 DAI NO and only yesGNO.
| regular price | 60 | |||||
| price yes | 63 | |||||
| likelihood yes | 60.00% | |||||
| DAI | DAIYes | DAINO | GNOYES | GNONO | GNO | |
| DAI | 1 | 1.666666667 | 2.5 | 0.02645502646 | 0.04504504505 | 0.01666666667 |
| DAIYES | 0.6 | 1 | 0.6666666667 | 0.01587301587 | 37 | 100 |
| DAINO | 0.4 | 1.5 | 1 | 94.5 | 0.01801801802 | 150 |
| GNOYES | 37.8 | 63 | 0.01058201058 | 1 | 0.5873015873 | 1.587301587 |
| GNONO | 22.2 | 0.02702702703 | 55.5 | 1.702702703 | 1 | 2.702702703 |
| GNO | 60 | 0.01 | 0.006666666667 | 0.63 | 0.37 | 1 |